
 |
ゲームの楽しみ
お正月の楽しみはさまざまですが、私が子供の頃は、大人も子供も一緒になって素朴なゲームに夢中になったものです。例えば、双六(すごろく)。本来の双六はちょっと違ったゲームだったようですが、サイコロを振って、出た目の数だけ進み、早くゴールした人の勝ちという簡単な遊びです。ゴール直前で振り出しに戻された涙目の子供には、サイコロを二回振ることのできる特権がありました。ところで、皆さん、サイコロを二回振るのと、一回だけ振って出た目の二倍進ませてもらうのと、選べるとしたらどちらを取りますか。  数学、それは考えて、考えて、 楽しむこと 私は、大学で数学を教え、数学の研究を志しています。数学というと、学校の教科や選抜試験の科目としてのイメージから、どうしても嫌われ者の代名詞となりがちです。それは悲しく、残念なことです。数学は英語ではマテマティクス(mathematics)と言いますが、語源を遡ると、ギリシャ語のマテーマになるようです。それは知識とか科学を意味し、文字通りの「数の学問」とはちょっと違っています。数学の本来の姿は、「考えること」といえます。問題集を解かされるのは嫌でも、問題を作って考えることは楽しいものです。合否に関係なければ、数学の楽しみは身近にも広がっていることでしょう。 確率論の広がり サイコロや百発一中の砲のように偶然に左右される事象は確率を用いて考察します。歴史的にも確率論は賭け事の研究に始まったようです。十七世紀半ばに貴族から相談を受けた若いパスカルが、当代随一の数学者フェルマと始めた文通は有名です。その百年前、三次方程式の解の公式に名を残すカルダーノは『偶然のゲームに関する本』を著しました。ギャンブラーとして知られるカルダーノですから、相当真剣に研究したに違いありません。その後、確率論は微積分学と融合し、二十世紀に入ると時間とともに変動する偶然現象を対象とする確率過程論・確率微分方程式論として発展して、今に至っています。アポロ計画の下で、通信のノイズ除去を目指したフィルタリング理論が大きく発展しましたが、これは確率過程論に属する課題です。最近では、ウォールストリートで仕事をするなら「伊藤の公式」は必須アイテムとまで言われています。これは確率微分方程式論に属するかなり高度な数学公式です。 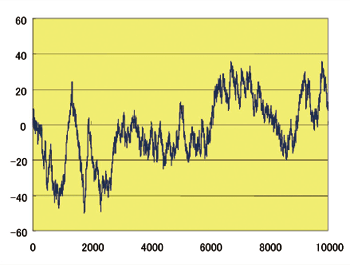 私の専門は、確率論の中でも、量子確率論(Quantum Probability)という新しい分野にあります。その名が示す通り、二十世紀に大発展した量子力学における統計的な問題にルーツを持ちます。物理学との関連は当初からの研究テーマですが、最近では、そこから派生した新しい考え方を複雑ネットワーク研究に応用することに力を注いでいます。生物の進化系統樹や家系図、ウェッブサイトの相互リンク、鉄道網や電話回線網、友人関係などを、点と線だけで表して得られる図形がネットワークです。実世界のネットワークは大きく複雑です。それらの数学モデルを考えて、分類したり、生成メカニズムを探ったり、あるいはネットワーク上を移動するときの時間とか効率を評価したり、さらにはそれをコントロールすることなどが大きな研究テーマです。量子力学とは何の関係もない世界の問題なのですが、量子確率論から生まれた新しいアイデアがいろいろな形で役立つのです。ある研究テーマの下で見つかった考え方が、直接関係のない別の分野の問題に適用できて、その世界がどんどん広がってゆくところ、それは数学のもつ醍醐味の一つです。 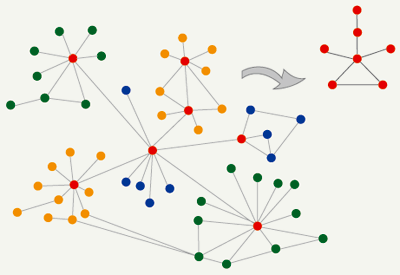 応用数学連携フォーラムの試み 今、数学は転換期を迎えていると思います。数学が自己充足に陥らず、他分野との研究交流の中に発展のエネルギーを求め、さらに、数学をもっと直接的に他分野の問題解決に応用する機運がこれまでになく高まっています。数学の定理として示された美しい配列を実験家に提案して、化学合成の実現可能性を探る研究など新しい動きが出てきています。複雑化する現代社会の中で私たちが直面するさまざまな問題の解決のためには、諸分野の連携や協同が必要であることは皆が認めていますが、その中にあって数学の果たす役割にも高い期待が寄せられてきています。数学は科学の共通言語とも言われます。個別の問題に対して作った数学モデルが別の問題に応用され、そこに見出された共通の構造が普遍的な理論に発展するような柔軟性は数学の特徴です。
|
 |
尾畑 伸明(おばた のぶあき) |